STOP PRESS

After recording our video The Problem with Powers of Two, further progress was made…

OEIS founder Neil Sloane reports:

On March 6, 2022, correspondent M.S.Smith sent me an email with a new theorem that essentially solves the problem!

In an instant we went from knowing almost nothing to knowing a very great deal. The problem isn't fully solved, but now we know the solutions for all n up to 9, we have a good asymptotic bound, and the problem has gone from being impossibly hard to one where we can get very close to the right answer by a routine calculation.

This is a brilliant piece of work, since some of the best number theorists in the world had failed to solve it when it was posted to various mailing lists.

Here is what Smith did.

Write the n numbers around a clock dial (see the drawing).

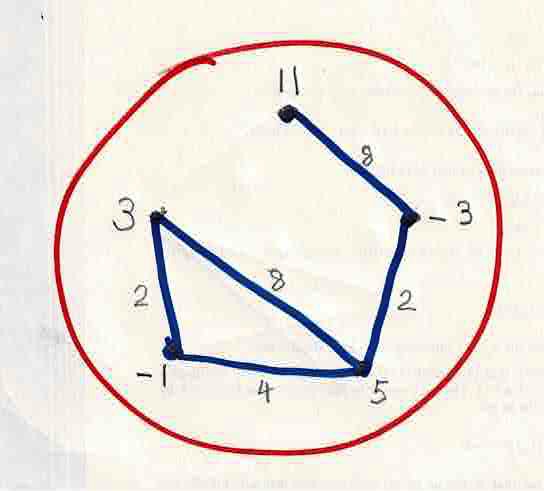
Draw a straight line between two numbers if they add up to a power of 2.

Smith showed that this network (or graph) cannot contain a closed path of 4 lines.

You can't have 4 numbers with u joined to v joined to w joined to x joined back to u.

Now the question of finding the biggest graph with n vertices and not containing a closed path of 4 lines is something we know a lot about. It has been studied for over 70 years.

By using what was known about that problem, Smith was able to solve the Problem of the Week for up through 9 numbers, and for 10 numbers to show that the answer is either 15 or 16. We now also have a rigorous upper bound for any any number of numbers.

The main thing though is that Smith has changed a problem that seemed beyond hope to a problem where we can get very close by solving a routine problem in graph theory. Absolutely brilliant!

(see sequence A006855 in the OEIS)